Iterating Over Binary Trees

Binary trees are great. If you ever have to implement one yourself though, you're probably either using C or you need to look at the documentation for your language's standard library more closely. Even POSIX C has the tsearch family of functions from <search.h>.

Recently I found myself attempting to implement a bootstrapping compiler in a rather restrictive subset of Java, and found the need for some kind of associative array data structure. I chose a splay tree, because, well, I like them.

Soon I found that I wanted the ability to iterate over the entire tree, in sorted order. This ability is provided by C++'s std::map::iterators, for example. I considered using a threaded tree, then an iterator holding a stack, before I realised that there is a much simpler solution with equal performance. It requires only that the nodes store a reference to their parent node, which mine could with little extra effort.

The principle is simple. If a node has a right subtree, its successor is the minimal (leftmost) node in that subtree. Otherwise, its successor is the parent of its first ancestor which is not a right child. In code,

public class Node {
    private Node left, right;

    public Node next() {
        Node next;

        if (right == null) {
            // Node has no right child
            next = this;
            while (next.parent != null && next == next.parent.right) {
                next = next.parent
            }
            next = next.parent;
        } else {
            // Find the leftmost node in the right subtree
            next = right;
            while (next.left != null) {
                next = next.left;
            }
        }

        return next;
    }
}

But how fast is this? An individual call to node.next() could traverse from the bottom to the top of the tree, at a cost of $O(h)$, where $h$ is the height of the tree. If there are $n$ nodes in the tree, could we traverse $O(n h)$ edges to visit the whole tree? This would be particularly bad for a splay tree, which is not necessarily balanced at any given time.

It turns out that we need only traverse $O(n)$ edges to visit the entire tree. For an informal proof, note that our algorithm is basically equivalent to tracing an outline of the tree like this:

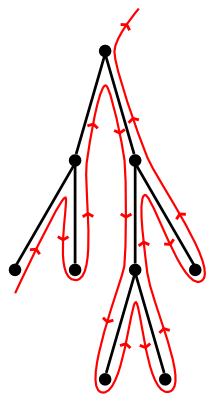
Clearly we can only trace around any edge at most twice (on its left and right side). Since any tree has $n - 1$ edges, we traverse at most $2 (n - 1) \in O(n)$ edges in the process of exploring the whole tree.